Đề bài
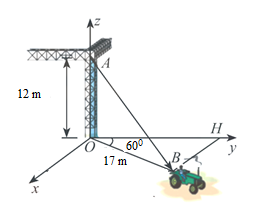
Một chiếc xe đang kéo căng sợi dây cáp $AB$ trong công trường xây dựng. Trên đó đã thiết lập hệ toạ độ $Oxyz$ như hình vẽ với độ dài đơn vị trên các trục tọa độ bằng $1~m$. Biết $OB = 17m$, $OA = 12m$ và $\widehat{HOB} = 60^{0}$. Giả sử tọa độ của vectơ $\overset{\rightarrow}{AB} = \left( {a;b;c} \right)$, tính $P = b + c$.
Phương pháp giải
Áp dụng biểu thức tọa độ các phép toán vecto.
Lời giải chi tiết
Ta có \(\overrightarrow {OA} = 10\vec k \Rightarrow A(0;0;12)\).
Xét \(\Delta OBH\) có \(OH = OB \cdot \cos {60^o } = \frac{{17}}{2}\).
\(OK = BH = OB \cdot \sin {60^o} = \frac{{17\sqrt 3 }}{2}\).
\( \Rightarrow {\rm{ }}B\left( {\frac{{17\sqrt 3 }}{2};\frac{{17\sqrt 3 }}{2};0} \right) \Rightarrow \overrightarrow {AB} = \left( {\frac{{17\sqrt 3 }}{2};\frac{{17}}{2}; - 12} \right)\).
Vậy \(P = b + c = \frac{{17}}{2} - 12 = - 3,5\).